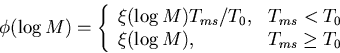 |
(1) |
We can model the IMF as a broken power law as in equation (32) of Miller & Scalo (1979) [henceforth MS],
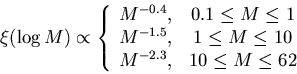 |
(2) |
I will assume that Tms=T0 for ![]() , and that
, and that
![]() to get
to get
| Tms/T0 = M-2.5. | (3) |
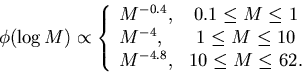 |
(4) |
Now we need to convert this into a magnitude distribution.
I will assume that ![]() .
Luminosity is related to absolute magnitude by
.
Luminosity is related to absolute magnitude by
![]() so
so
| |
(5) |
| |
(6) |
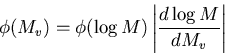 |
(7) |
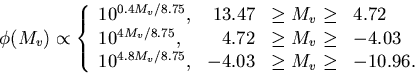 |
(8) |
(Note: a shortcut is to take the luminosity function of stars per unit absolute magnitude per pc3 directly from Figure 1 of MS.)
If we normalize equation(8)
so that ![]() and that
the power-law segments are continuous at the boundaries, we find
and that
the power-law segments are continuous at the boundaries, we find
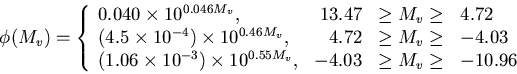 |
(9) |
In order to convert this from a distribution in absolute magnitude (Mv) to a distribution in apparent magnitude (mv) and distance (d) we need the relation
![]()
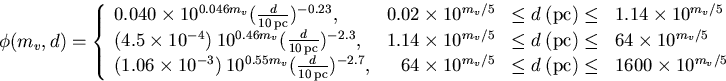 |
(10) |
To get the total magnitude distribution, we need to integrate this over the volume of space seen in 1 square degree. This integral has the following form:
| |
(11) |
To determine ![]() , I will assume that the stellar
density decreases exponentially as a function of Galactic radius, and
also falls off exponentially with distance from the midplane of the
disk, so
, I will assume that the stellar
density decreases exponentially as a function of Galactic radius, and
also falls off exponentially with distance from the midplane of the
disk, so
| |
(12) |
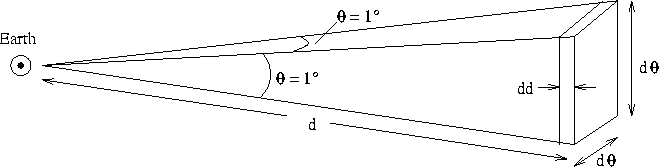
The volume integral is over the volume seen in one square degree. As we go further out in d, the cross-sectional area increases, as shown in Figure 1. The volume element dV can be rewritten as
| (13) |
Some if you integrated ![]() with
with ![]() and
and ![]() .This is incorrect. See the Appendix for the correct
way to do it.
.This is incorrect. See the Appendix for the correct
way to do it.
Thus, equation (11) becomes
- (a)
- Toward the Galactic center:
If the distance from the earth/sun is d and the distance from the
Galactic center is r, then as we move toward the Galactic center,
r=8-d kpc. Past the Galactic center, r=d-8 kpc. Substituting
into the equation for
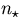 and taking z=0,
and taking z=0,
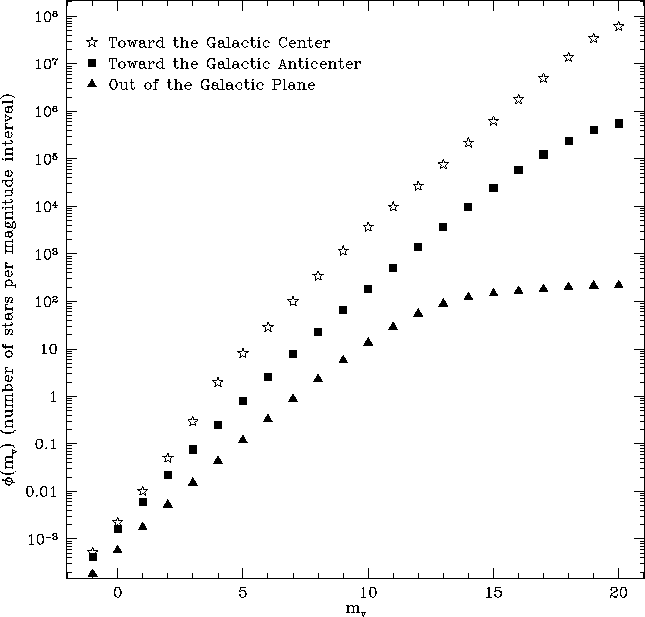
Note: d needs to be converted to parsecs to be consistent with the units used in the integral.The resulting distribution (via Mathematica) is plotted in Fig. 2 as stars.
- (b)
- Toward the Galactic anticenter:
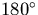 away from Galactic center, d=r+8 kpc, so
away from Galactic center, d=r+8 kpc, so
where d is in pc.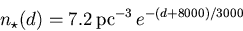
(14) The resulting distribution (via Mathematica) is plotted in Fig. 2 as squares.
- (c)
- Directly overhead:
Here, r=8 kpc is constant and z changes:
where z0 is 180 pc.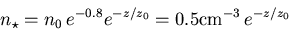
(15) The resulting distribution (via Mathematica) is plotted in Fig. 2 as triangles.
For this problem, we just integrate the functions calculated in
Problem 1 for ![]() . I will also choose an arbitrary
minimum magnitude of
. I will also choose an arbitrary
minimum magnitude of ![]() , since the brightest star
visible from earth has a visual magnitude of -1.
(Really, if your lower limit is between -1 and
, since the brightest star
visible from earth has a visual magnitude of -1.
(Really, if your lower limit is between -1 and ![]() , your
answer shouldn't be affected too much.)
, your
answer shouldn't be affected too much.)
- (a)
- Toward the Galactic center:
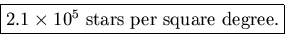
- (b)
 away from Galactic center:
away from Galactic center:
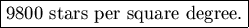
- (c)
- Directly overhead:
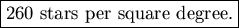
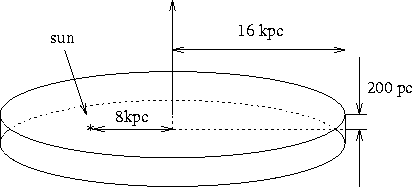
Let's assume that the average HI number density in the solar neighborhood is
![]() . From §9.2 of Binney & Merrifield, the distribution
of HI is approximately uniform out to 16 kpc from the center
of the Galaxy. So, let's assume that the gas in uniform in the radial
direction, and falls off exponentially with radius with
a scale height of 200 pc. (See Fig. 3 for illustration.)
Then,
. From §9.2 of Binney & Merrifield, the distribution
of HI is approximately uniform out to 16 kpc from the center
of the Galaxy. So, let's assume that the gas in uniform in the radial
direction, and falls off exponentially with radius with
a scale height of 200 pc. (See Fig. 3 for illustration.)
Then,
| (16) |
The column density along a given line of sight is
| (17) |
- (a)
- Toward the Galactic center
In the Galactic plane, nH is constant. Thus,
The total column length toward the Galactic center is![\begin{displaymath}
N_H = n_H\ell
= 1\,\mathrm{cm}^{-3} \times \ell \times \fra...
...m}}{\pc}
= (3.1 \times 10^{18} \mathrm{cm}^{-2})\: \ell [\pc] \end{displaymath}](img51.gif)
(18) 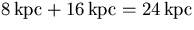 . So the total column density is
. So the total column density is
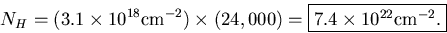
- (b)
 away from Galactic center
away from Galactic center
This line of sight is also in the Galactic plane so we can use Equation (20). Away from the Galactic center,
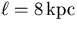 so
so
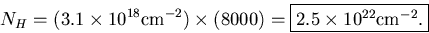
- (c)
- Directly overhead
Out of the plane of the Galaxy,
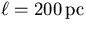 so
so
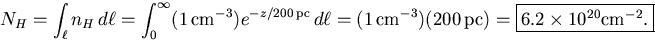
| |
(19) |
- (a)
- Per kpc:
- i. & ii.
- In the plane of the Galaxy, we derive the extinction per kpc
from Equation (20).
In 1 kpc, the column density is
so the extinction per kpc is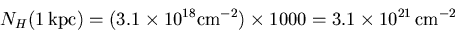
toward both the Galactic center and anticenter.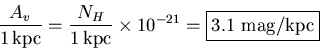
- iii.
- Out of the plane of the Galaxy, we can define the
extinction per kpc as
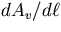 where
where  is in units
of kpc.
is in units
of kpc.
- (b)
- in total:
For this part, we can simply take the total column densities calculated in Problem 3 and plug into Equation (21).
- i.
- Toward the Galactic center
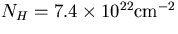 so
so
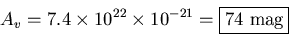
- ii.
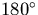 away from Galactic center
away from Galactic center
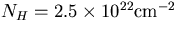 so
so
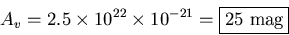
- iii.
- Directly overhead
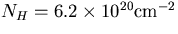 so
so
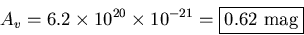
First, we should find the position of the Taurus clouds in terms of
galactic coordinates. Taurus is at ![]() and the conversion to galactic coordinates is
and the conversion to galactic coordinates is
- (a)
- How many stars per square degree could he expect without
the ``extra'' extinction due to his ``dark nebulae?''
This calculation is similar to Problem 2, but we have to take two things
into account: (1) the line of sight, which is non-trivial, and (2)
extinction as described in Problem 4.
The line of sight is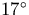 out of the plane of the Galaxy,
and
out of the plane of the Galaxy,
and 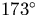 offset from the Galactic center (see Fig. 4).
We can decompose d into its projections onto the plane of the
galaxy and the z-axis. From Fig. 4,
offset from the Galactic center (see Fig. 4).
We can decompose d into its projections onto the plane of the
galaxy and the z-axis. From Fig. 4,
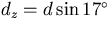 and
and 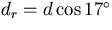 .
In particular,
.
In particular,
To calculate r, you can do some more trigonometry, saying that r is the third side of a triangle with sides 8 kpc and dr with an interior angle of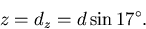
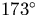 , and get
, and get
or you can say that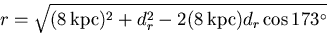
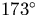 is awfully close to
is awfully close to 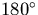 ,
and
,
and
I will opt for the latter. Thus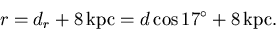
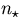 is
is
![\begin{displaymath}
n_\star(d) = n_0 e^{-r/r_0-z/z_0}
= (7.2\,\pc^{-3})\exp\lef...
...pc}}{3\,\mathrm{kpc}}
-\frac{d\sin17^{\circ}}{180\,\pc}\right]\end{displaymath}](img81.gif)
The increase in apparent magnitude due to extinction is simply the Av calculated in Problem 4. So,
The integral we need to solve looks like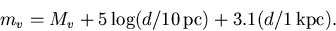
(20) 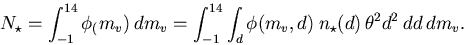
(21) After plugging into my numerical integrator (Mathematica) I find
 with no extinction
with no extinction
and
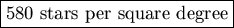 including extinction.
including extinction.
- (b)
- How much extinction would be associated with ``almost black'' and
``totally black'' regions?
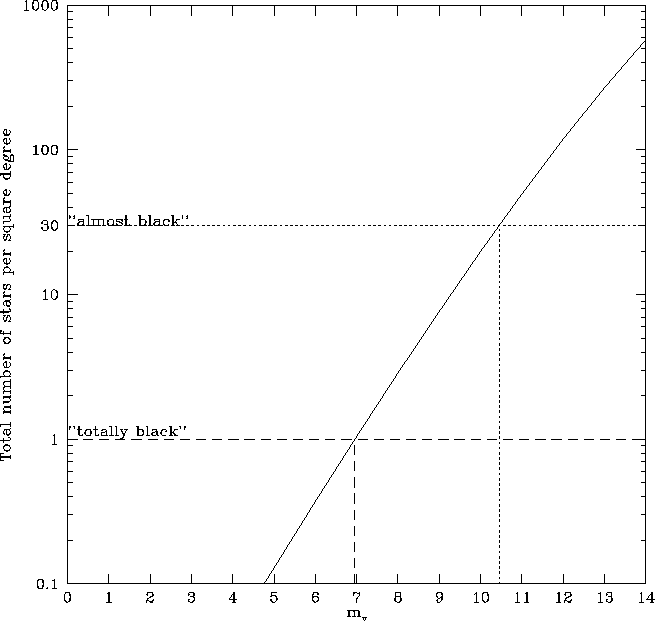
I have plotted the cumulative number of stars visible out to a a magnitude mv in Figure 5. Additional extinction due to the Taurus clouds has the effect of shifting this curve to the right, or to higher magnitude.
- i.
- ``almost black'' regions:
Barnard's ``almost black'' have approximately 30 stars per square degree.
Looking at Fig. 5, we see 30 stars per square degree up to a
limiting magnitude of about 10.4. Thus the extra extinction is
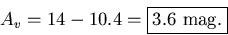
- ii.
- ``totally black'' regions:
Let's say the cutoff for a ``totally black'' region is 1 star per square degree. Then Fig. 5 indicates that a limiting magnitude of about 7 is appropriate. Thus