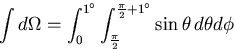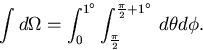Next: References
Up: No Title
Previous: No Title
What is a solid angle of 1 square degree (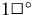 )?
This is this the solid angle encompassed by taking 1 degree in one
direction by 1 degree in the perpendicular direction.
In other words,
)?
This is this the solid angle encompassed by taking 1 degree in one
direction by 1 degree in the perpendicular direction.
In other words,
| 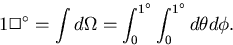 |
(22) |
If you simply integrate over the solid angle
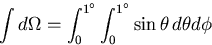
you will get the wrong answer. This solid angle is shown in
Fig. 6.
Figure 6:
Figure 7:
![\begin{figure}
\begin{minipage}[b]
{2.5in}
\epsfig {file=solidangle.eps}
\end{m...
...\begin{minipage}[b]
{3.5in}
\epsfig {file=sqdeg.eps}
\end{minipage}\end{figure}](img92.gif) |
The correct limits to use are
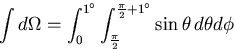
which is shown in Fig. 7.
Converting degrees to radians, 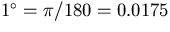 radians.
Now
radians.
Now 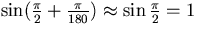 .So, we can rewrite the solid angle as
.So, we can rewrite the solid angle as
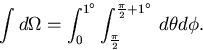
Shifting the limits on 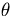 by
by 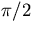 , we see that this is the same
as Equation (28).
, we see that this is the same
as Equation (28).
Hannah Jang-Condell
10/31/2000
![]()